The dishes problem

Problem: "How many guests are there?" said the official. "I don't know," said the cook, "but every 2 used a dish of rice, every 3 used a dish of broth, and every 4 used a dish of meat between them". There were 65 dishes in all. 

The way I solved this problem without algebra is to consider how many dishes are used following a lowest common multiple of people, ie. 12. So 12 guests minimum use 13 dishes total. 13 dishes per 65 total dishes equals 5. Taking 5 by 12 guests gives the result 60 guests. 

I think offering examples of math problems to students from different cultures can be worthwhile as it encourages students to think beyond their current cultural lens. Math history from different cultures can be especially important as it offers an opportunity to see how different cultures come up with different solutions to the same problem. I enjoy having imagery to math word problems and puzzles as it gives it allows me to make a realistic connection. This dishes problem is extremely relevant in Asian cultures as Asian cuisines often involve large banquets around a table consisting of family and friends. 

Goldberg Polyhedron Powerpoint

https://docs.google.com/presentation/d/12PvoQ9RdoHqTRYqzulqU2y3_30tHfmFhlL7J_g38WSU/edit?usp=sharing

Goldberg Polyhedrons

In geometry, a polyhedron is a 3D shape with polygon faces, straight edges, and sharp corners or vertices. It derives from the Greek word “many-base.” Polyhedrons are convex, meaning that their faces are curved outward. A Goldberg polyhedron is a convex polyhedron made of pentagon or hexagon faces, ie. five or six sided polygons and exactly three faces meet at each vertex.

 Goldberg Polyhedrons have notation of the form GP(x,y), where x is the number of steps in one direction, and y is the number of steps taken after turned 60^o. We can use x, y to calculate the triangulation number, T, where T = x² + xy + y² = (x+y)² – xy. Multiplying the triangulation number and the number of original faces the polyhedron has will determine the number of triangles the new polyhedron will have. This process is a type of subdivision known as principal polyhedral triangle (PPT), which breaks down the structure of a polyhedron. By subdividing the Goldberg polyhedron and slicing the spherical shape in half, we create a geodesic dome. The triangular shapes are structurally rigid and create a sturdy and durable structure. Any pressure applied to one triangle is evenly distributed to other triangles.  

Figure 1:  A GP(5,5) Goldberg Polyhedron (left).

Figure 2: A GP(5,5) subdivided by triangulation number (left). 

For this project, I tried to recreate creating several different kinds of Goldberg polyhedrons by colouring golf balls. The divots in the golf balls are all hexagon shaped. A problem I ran into while working on this project, was that divots were not entirely uniform, ie. same size. Nonetheless, it was an interesting opportunity to try and draw my own Goldberg polyhedron. An extension of this activity in the classroom could be to give students toothpicks and marshmallows and challenge them to first create a Goldberg polyhedron, then subdivide the faces to create a geodesic dome and compare strengths between their creations. This activity teaches students teamwork and cooperation, but also lets them explore and experiment on creating integral structures resistant to falling. There is another interesting resource online that is found on https://levskaya.github.io/polyhedronisme/, which generates different polyhedrons. It would be useful to integrate this resource in the digital classroom as it is a great visualization tool that demonstrates easily how polyhedrons change when different operators are applied such as truncating, orthogonality, duality, reflecting and snubbing. 

Figure 3: A GP(5,0) created from a golf ball. 

Figure 4: Virtual recreation of Fathauer's Goldberg Polyhedron using polyHedronisme. 

This was my first group project since starting the teacher education program at UBC, and I had a blast. I’ve learned so much through creating Goldberg polyhedral patterns on golf balls and researching polyhedrons. My favourite part of this project would be the interactive session using polyHedronisme. As a teacher, I hope to integrate many different digital tools in the classroom for learning. We are living in such a technologically advanced generation, I feel that incorporating these technologies into the classroom can be opportunities for students to engage with mathematics on a deeper level than equations seen in a textbook. 

Sources:

Fathauer, R. 2019. Robert Fathauer. Retrieved September 27, 2020 from http://gallery.bridgesmathart.org/exhibitions/2020-bridges-conference/fathauer. 

Hart, G.W. n.d. A Twelve-Part Puzzle Based on the (4,2) Goldberg Polyhedron “Tectonic Plates.”  Retrieved September 27, 2020 from https://georgehart.com/puzzles/GBpuzzle-4-2/goldberg-puzzle-2.html. 

Levskaya, A. 2019. polyHedronisme. Retrieved September 27, 2020 from https://levskaya.github.io/polyhedronisme/.

Mathematical understanding and multiple representations

Pape and Tchnoshanov argue that helping students utilize internal and external representation of mathematical concepts are important at interpreting physical, social and mathematical phenomena and can be beneficial to student learning experience. I agree that multiple representations facilitate student development of math concepts. When students are taught different forms of representational mathematics, they may be able to use internal representations to organize ideas and solve problems. Then they can transform those cognitive schemas to external representations such as tables, graphs and diagrams as tools to draw ideas and inferences to facilitate argument and support conclusions. I also agree that teaching students in different instructional styles to be beneficial to encourage sharing of ideas and communication of math concepts. For example, some students may prefer pure-analytic approach to solving problems while others take on a visual style. Students can be introduced to explore alternative ways of reasoning and inquiry when learning to solve problems, which encourages creativity to problem solving. They are also more likely to share ideas to students who solved problems differently.

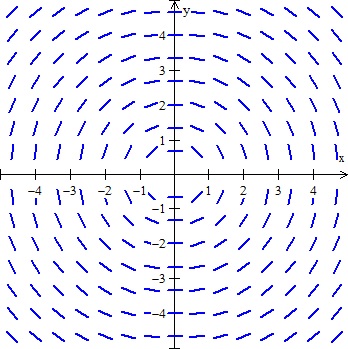
One form of mathematical representation that interested me while learning was on slope fields, which is a visual representation of a differential equation solution. Slope fields can also tell information on stability of an equation. This is could be a useful tool when teaching students AP Calculus as it could help students visualize how differential equations behave. I can teach the students how to use this tool analytically at first by creating tables of values and sketching them out, but I can also integrate web tools like Desmos to show slope fields quicker.  

Slope field for dy/dx = -x/y

 

Paper: Pape S.J., Tchoshanov M.A. 2001. The Role of Representation(s) in Developing Mathematical Understanding. Theory into Practice. Vol. 40, No. 2. Pp. 118-127

The kind of teacher I want to be

My favourite math teacher is a teacher I had for several years from grade 9 to 11. My favourite thing about him was his teaching style; he taught instrumental learning very well through detailed examples and clear notes. He had a very friendly personality and had a very good humour which made his classroom a safe and welcoming environment. He made himself readily available for help afterschool most days or during tutorial hours, but also uploaded class notes to his website which made it easy to review missed material or a resource to go to for clarification. My least favourite math teacher was a prof I had for introductory Number Theory because it was difficult to follow along with his lectures as proofs skipped lots of steps and weren’t very intuitive. Often, it was difficult to read and felt rushed. Assessment of learning did not feel fair, as only unspecified questions in the problem set would be marked; I could have understood all questions in the problem set except for one and if that one question is selected for grading, it would be an unfair representation of my understanding of the material.

 

Letter #1, the student who liked me:

Hi Mr. Y,

Do you remember me? I was the student you had a few years ago who started off the year struggling but with your patience, persistence and help, I managed to finish off the year with 86%. You made every class enjoyable to attend because your humour and relevance to teaching made learning fun. I saw real-world application of what we were learning in class in other subjects like economics and art. My favourite part of coming to class was how you greeted everyone individually at the door as the 9am bell rang. You made tests fair by testing us on things we learned and no “surprises.” Anyways, I had so much fun being in your class and hope to visit you soon,

Student A.

Letter #2, the student who disliked me: 

Mr. Y,

I hated your class. Your math class was the hardest class to sit through every day. I’m not sure if you had a lot on your plate, but it seemed like you had to review your notes often before or even while you’re teaching, so sometimes you make class confusing. You emphasized how there are multiple ways to solve problems, which confuses me. I just want to know how to solve problems one way and always use one way. I also think you assign too many practice problems.

From,

Student B.

Discussion on Skemp

I agree with Zach, Jeff, Cheryl, Yiwen and Karishma’s group response on ways to improve the negative attitudes of math anxiety. It is important as math educators to work at eliminating the negative stigma associated with math; I feel that students develop negative attitudes towards math due to negative experiences or disinterest in the subject. I agree with the idea of providing formula sheets during tests so that we can step away from requiring students to memorize mathematics, but rather think critically and apply concepts to solve different problems. I also like the idea of having easy quizzes at the beginning of class to keep up with content and test understanding before progressing, however I would choose not to call them quizzes as that might evoke some anxiety and stress on students feeling like they need to perform well on them. As math is such a cumulative subject, knowing where students stand on learning before progressing to another topic is important, so they do not fall very far behind in math learning. One thing I would like to add, is by being a supportive teacher and offering opportunities for one-on-one help can be valuable to the student to minimize negative attitudes to math anxiety as it demonstrates the teacher is a caring individual concerned for the student’s learning.

The 1000 locker problem

When attempting to solve this problem, I began by rewording the information provided. I then drew pictures to help visualize the problem. I defined ‘O’ to be an open locker and ‘X’ to be a closed locker. I also defined student 0 to be the initial state of the lockers before student 1 closes them. After drawing locker changes up to student 4, and extending the lockers altered to locker 15, I began to write out patterns I saw. For example:

I saw that locker 2 was opened 1000 times (student 0, 2, 3, …, 1000) and closed once (student 1).

I saw that locker 4 was open twice (student 0 and student 2) and closed everywhere else (student 1, 3, 4, 5, …, 1000) for a total of 999 times.

I saw that locker 9 was opened 7 times (student 0, 3, 4, 5, 6, 7, 8) and closed 994 times (student 1, 2, 9, 10, 11, …, 1000).

I saw that locker 15 was opened 989 times (student 0, 3, 4, 15, 16, 17, …, 1000) and closed 12 times (student 1, 2, 5, 6, 7, …, 14).

From here, I saw a pattern and came up with the conjecture which states: “lockers opened an odd number of times will be open at the end [after the 1000^th student].” At the time of working on the problem, I wanted to conduct a few more tests to verify the conjecture:

Consider locker 18. It was opened 988 times (student 0, 2, 6, 7, 8, 18, 19, …, 1000) and closed 13 times (student 1, 3, 4, 5, 9, 10, 11, 12, … ,17). 

This counterexample showed that the conjecture was false as locker 18 was opened an even number of times and remains open after the 1000^th student. As I am writing this blog now, I immediately see that this conjecture is false by the counterexample of locker 9 as the locker was opened an odd number of times but remains closed.

I then noticed that factors of the locker numbers were related to whether they were opened or closed, so I began listing out factors. I discovered that the lockers with an even number of factors would be open and the lockers with an odd number of factors would be closed. The only time a number would have an odd number of factors is if it was a perfect square. As the first 31 perfect squares are below 1000, that led me to conclude that there would be 31 lockers closed and 969 lockers open after all 1000 students had gone through opening and closing.

Skemp's two approaches to teaching and learning math

Skemp’s paper on comparing relational and instrumental understanding in mathematics was philosophical and interesting, however there were a few moments that made me stop and think when reading. Skemp defines instrumental understanding as learning “rules without reasons” while relational understanding is more knowing what to do and why.

The first moment that made me stop and reflect was when Skemp mentions one of the mismatches in mathematical learning, where a student’s goal is to understand instrumentally when the teacher wants them to learn relationally. This is extremely evident throughout my undergrad studies of mathematics, where the prof would spend a long time going over the proof and theory behind an equation, but it would be completely overlooked as the proof is more complicated than the equation. When I taught students math, they also only cared more about the equation as it would lead to the right answer quicker than understanding why the equation works; an advantage of instrumental understanding as mentioned by Skemp. The second moment which made me stop and think was when Skemp listed the advantages of relational mathematics, several of which were it being more adaptive to new tasks and being easier to remember. I noticed that with relational understanding, students draw conclusions on new (but similar) questions based on their previous learning as they see similarities in the questions. For example, I had students use the area of a triangular prism to solve for the area of a pyramid. Both shapes are similar but are different enough to require a different equation to solve for the area. The third moment I stopped while reading was when Skemp discussed the “over-burdened syllabi” where a single line of math contains many concentrated ideas. For example, Pythagorean Theorem is the sum of two small squares equals the big one. A student would have to draw out two squares, square their lengths, add them, and take the square root of that to find that diagonal line. In instrumental understanding, that would be the equation a²+b²=c²_.

Skemp argues that relational understanding would take too long to achieve and may be too difficult depending on the topic. I agree, however believe the advantages of relational understanding outweigh the disadvantages. Teaching students the theory behind an equation and why it works can get them to ask questions and think outside the box; which are important aspects to learning and critical thinking.

Paper: Skemp, R. Relational understanding and instrumental learning. Mathematics Teaching, 77, 20-26, (1976)

First post!