Mathematical understanding and multiple representations

Pape and Tchnoshanov argue that helping students utilize internal and external representation of mathematical concepts are important at interpreting physical, social and mathematical phenomena and can be beneficial to student learning experience. I agree that multiple representations facilitate student development of math concepts. When students are taught different forms of representational mathematics, they may be able to use internal representations to organize ideas and solve problems. Then they can transform those cognitive schemas to external representations such as tables, graphs and diagrams as tools to draw ideas and inferences to facilitate argument and support conclusions. I also agree that teaching students in different instructional styles to be beneficial to encourage sharing of ideas and communication of math concepts. For example, some students may prefer pure-analytic approach to solving problems while others take on a visual style. Students can be introduced to explore alternative ways of reasoning and inquiry when learning to solve problems, which encourages creativity to problem solving. They are also more likely to share ideas to students who solved problems differently.

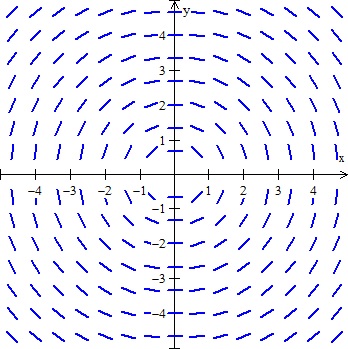
One form of mathematical representation that interested me while learning was on slope fields, which is a visual representation of a differential equation solution. Slope fields can also tell information on stability of an equation. This is could be a useful tool when teaching students AP Calculus as it could help students visualize how differential equations behave. I can teach the students how to use this tool analytically at first by creating tables of values and sketching them out, but I can also integrate web tools like Desmos to show slope fields quicker.  

Slope field for dy/dx = -x/y

 

Paper: Pape S.J., Tchoshanov M.A. 2001. The Role of Representation(s) in Developing Mathematical Understanding. Theory into Practice. Vol. 40, No. 2. Pp. 118-127